Una matriz es una tabla cuadrada o rectangular de datos (llamados elementos o entradas de la matriz) ordenados en filas y columnas, donde una fila es cada una de las líneas horizontales de la matriz y una columna es cada una de las líneas verticales. A una matriz con m filas y n columnas se le denomina matriz m-por-n (escrito m×n), y a m y n dimensiones de la matriz. Las dimensiones de una matriz siempre se dan con el número de filas primero y el número de columnas después. Comúnmente se dice que una matriz m-por-n tiene un orden de m × n ("orden" tiene el significado de tamaño).
CLASES DE MATRIZ:
Matriz cuadrada: es una matriz que tiene el mismo número de filas que de columnas. El conjunto de todas las matrices cuadradas n-por-n junto a la suma y la multiplicación de matrices, es un anillo que generalmente no es conmutativo.
M(n,R), el anillo de las matrices cuadradas reales, es un álgebra asociativa real unitaria. M(n,C), el anillo de las matrices cuadradas complejas, es un álgebra asociativa compleja.
Matriz identidad In: de orden n es la matriz n por n en la cual todos los elementos de la diagonal principal son iguales a 1 y todos los demás elementos son iguales a 0. La matriz identidad se denomina así porque satisface las ecuaciones MIn = M y InN = N para cualquier matriz M m por n y N n por k. Por ejemplo, si n = 3:
La matriz identidad es el elemento unitario en el anillo de matrices cuadradas
El primer número nos indica el número de filas que tiene la matriz.
El segundo indica la cantidad de columnas que tiene la matriz.
Ejemplo:
Si la matriz es A las posiciones de cada número son ai j
i es la fila y j es la columna donde se encuentra posicionado el número en la matriz A.
Si la matriz es B las posiciones de cada número son bi j
i es la fila y j es la columna donde se encuentra posicionado el número en la matriz B.
EJEMPLO:
OPERACIONES BASICAS.
Suma y adicción.
Dadas las matrices m-por-n ,A y B, su suma A + B es la matriz m-por-n calculada sumando los elementos correspondientes (i.e. (A + B)[i, j] = A[i, j] + B[i, j] ). Es decir, sumar cada uno de los elementos homólogos de las matrices a sumar.
Para poder sumar matrices deben de tener el mismo orden, ambas matrices deben tener el mismo número de filas y columnas.
Entonces Si A = (ai j) mxn y B = (bi j) mxn entonces su suma es A + B = (ai j + bi j) mxn.
Ejemplo:
PROPIEDADES
• Asociativa
Dadas las matrices m×n A, B y C
A + (B + C) = (A + B) + C
• Conmutativa
Dadas las matrices m×n A y B
A + B = B + A
• Existencia de matriz cero o matriz nula
A + 0 = 0 + A = A
• Existencia de matriz opuesta
con gr-A = [-aij]
A + (-A) = 0
Inverso aditivo (resta).
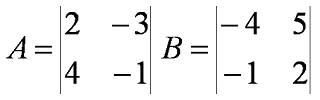
Operación A-B
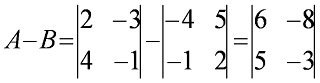
El orden es igual que en la suma pero se debe tener en cuenta los signos.
PRODUCTO POR UN ESCALAR
Dada una matriz A de m filas y n columnas, lo que podemos denotar como:
la multiplicación de A por un escalar k, que se denota k•A, k×A o simplemente kA, está definida como:
es decir, corresponde a la matriz conformada por cada elemento de la matriz multiplicado por dicho escalar.
Ejemplo.
2A .
La multiplicación por escalar es análoga a la suma o resta de matrices, y cumple con las mismas características de la multiplicación aritmética. En efecto, podemos llegar al mismo resultado sumando k veces la misma matriz A entre sí.
Propiedades.
Sean A, B matrices y c, d escalares, la multiplicación de matrices por escalares cumple con las siguientes propiedades
MULTIPLICACION DE MATRICES
Los resultados en las posiciones marcadas dependen de las filas y columnas de sus respectivos colores.
El producto de dos matrices se puede definir sólo si el número de columnas de la matriz izquierda es el mismo que el número de filas de la matriz derecha. Si A es una matriz m×n y B es una matriz n×p, entonces su producto matricial AB es la matriz m×p (m filas, p columnas) dada por:
la multiplicación de A por B, que se denota A•B, A×B o simplemente AB, está definida como:
donde cada elemento ci,j está definido por:
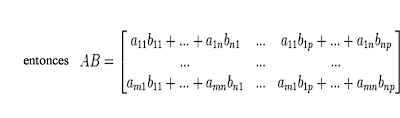
EJEMPLO.
Propiedades.
Sean A, B y C matrices para las cuales la multiplicación entre ellas está bien definida, es decir, tales que sus elementos pertenecen a un cuerpo donde la multiplicación está definida, y de manera que el número de filas y de columnas permite realizar la multiplicación; entonces se cumplen las siguientes propiedades:
El producto de dos matrices generalmente no es conmutativo, es decir, AB ≠ BA. La división entre matrices, es decir, la operación que podría producir el cociente A / B, no se encuentra definida. Sin embargo, existe el concepto de matriz inversa, sólo aplicable a las matrices cuadradas.
Transpuesta
Artículo principal: Matriz transpuesta
La transpuesta de una matriz m-por-n A es la matriz n-por-m AT (algunas veces denotada por At) formada al intercambiar las filas y columnas, i.e.
La transposición de matrices tiene las siguientes propiedades:
Si A describe una aplicación lineal respecto a dos bases, entonces la matriz AT describe la transpuesta de una aplicación lineal respecto a las bases del espacio dual.
APLICACIÓNES ECONOMICAS DE LAS MATRICES
Las matrices sirven para representar simples procesos de producción y Flujos de producción.
La matriz se aplica en el contexto insumo, procesos y producto. Sirve para planificar la evaluación de los proyectos sociales y medir impactos logrados, antes, durante, después y posterior a su ejecución.
Bibliografia.
http://es.wikipedia.org/wiki/Matriz_(matemática)




















